¿Cuál es la diferencia entre Integrales Definidas, Indefinidas e Impropias?

Artemiy Rovinski
28 jun
3 Min. de lectura

Actualizado: 4 jul

Si estás empezando a estudiar cálculo, probablemente ya te encontraste con una palabra que se repite sin cesar: integrales. Y de pronto no solo hay una “integral”, sino varios tipos: definidas, indefinidas e incluso unas llamadas integrales impropias.

¿Qué significan exactamente? ¿En qué se diferencian? ¿Y para qué sirve cada una?

En este blog vamos a resolver todas estas dudas paso a paso, con explicaciones claras pero rigurosas, para que entiendas bien de qué va cada una.

🧩 1. Integral Indefinida: El origen de todo

Cuando hablamos de una integral indefinida, nos referimos a una familia de funciones cuya derivada es la misma.

Por ejemplo:

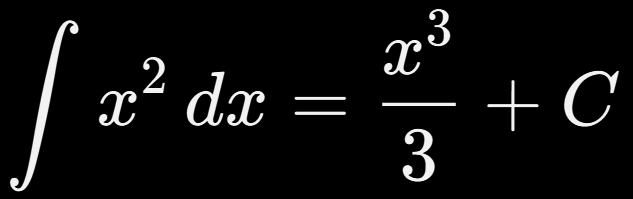
Ese +C es importante: como al derivar se “pierde” cualquier constante, la integral indefinida debe recuperar todas las posibles funciones primitivas.

👉 Se interpreta como la operación inversa de la derivada. Sirve principalmente para encontrar funciones originales antes de haber derivado, o para resolver ecuaciones diferenciales.

📐 2. Integral Definida: El área bajo la curva

Ahora, cuando colocamos límites superior e inferior en una integral:

estamos hablando de una integral definida.

Aquí no nos interesa obtener una función: lo que buscamos es un número real, que representa el área bajo la curva de f entre a y b.

Por ejemplo:

👉 Esta operación tiene aplicaciones concretas en física, economía, estadística, etc., donde necesitamos medir algo con precisión.

⚠️ 3. Integrales Impropias: ¿Qué pasa cuando el área no está bien definida?

Aquí llegamos al mundo de las Integrales Impropias, uno de los temas más sutiles e interesantes del cálculo integral.

¿Qué las hace “impropias”?

Las Integrales Impropias son aquellas en las que al menos una de estas dos cosas ocurre:

Uno (o ambos) de los límites de integración es infinito, como en:

La función tiene una discontinuidad o una “explosión” dentro del intervalo, como en:

En estos casos, la integral no puede evaluarse como una simple área tradicional, pero podemos intentar evaluarla como un límite.

Por ejemplo:

Aquí, el área sí es finita: la integral impropia converge. Pero hay muchas integrales impropias que divergen, es decir, no dan un valor finito.

🧠 ¿Por qué son tan importantes las Integrales Impropias?

Aunque parezcan “raras”, las Integrales Impropias tienen un papel fundamental en muchas ramas de las matemáticas:

En probabilidad, donde funciones densidad tienen soporte infinito.
En física, para modelar fenómenos infinitos o discontinuos (como cargas puntuales o campos eléctricos).
En análisis funcional, para construir transformadas como la de Fourier o Laplace.
Incluso en economía, donde a veces se integran variables que tienden al infinito en modelos teóricos.

Dominar las Integrales Impropias no es un lujo: es una necesidad para quienes quieren estudiar matemáticas de verdad.

✅ Recapitulando

Tipo de integral	¿Qué busca?	¿Qué da como resultado?	¿Cuándo se usa?
Indefinida	Recuperar una función original	Una familia de funciones (+C)	Para deshacer una derivada
Definida	Calcular área bajo una curva	Un número real	En aplicaciones físicas y concretas
Impropia	Medir áreas con límites infinitos o funciones mal portadas	Un número… si existe	En modelos teóricos, análisis, física