Cómo integrar por partes: una de las técnicas de integración más usadas en el cálculo integral
- Artemiy Rovinski
- hace 12 horas
- 2 Min. de lectura
¿Estás estudiando cálculo integral y te topaste con funciones que simplemente no se pueden integrar directo? Entonces es momento de aprender una de las herramientas más poderosas en el mundo de las integrales: la integración por partes.
Si alguna vez intentaste integrar algo como x·e^x y no supiste cómo, este blog es para ti. Te explicamos cómo funciona esta técnica paso a paso y cómo usarla como un verdadero matemático.
¿Qué es la integración por partes?
La fórmula de integración por partes es una forma de traducir la regla del producto de la derivada al mundo de las integrales. Es como “deshacer” la derivada de un producto.
Fórmula:

Aquí, dividimos la integral en dos partes:
Una función u, que será fácil derivar.
Una función dv, que será fácil integrar.
Luego usamos la fórmula, y muchas veces el resultado se vuelve más simple.
¿De dónde sale esta fórmula?
De la regla del producto de la derivada:

Si integramos ambos lados, obtenemos:

Reordenando:

Y eso es exactamente lo que usamos:

Ejemplo paso a paso:
Vamos a resolver:

Elegimos u y dv:
u = x → porque derivarla nos da 1.
dv = e^x dx → porque integrarla es muy fácil.
Derivamos u y integramos dv:
du = dx
v = e^x
Aplicamos la fórmula:
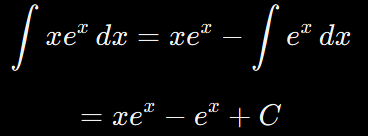
¡Listo! Hemos resuelto una integral que, sin esta técnica, parecería imposible.
¿Cómo elegir u y dv?
Un buen truco es seguir el acrónimo LIATE (Logarítmica, Inversa trigonométrica, Algebraica, Trigonométrica, Exponencial).Elige u como el primer tipo que aparezca en ese orden.
Por ejemplo:
En x·ln(x) → u = ln(x), dv = x dx
En x·cos(x) → u = x, dv = cos(x) dx
¿Cuándo se usa integración por partes?
Cada vez que tienes un producto de funciones, y:
Una se vuelve más simple al derivar.
La otra se integra fácilmente.
O incluso cuando no hay producto, pero puedes “inventarlo”. Por ejemplo:

Aquí puedes escribirlo como:

Y aplicar integración por partes.
Domina el Cálculo Integral desde cero con Mateguapo
Si este blog te ayudó a entender mejor la técnica de integración por partes, imagina lo que puedes lograr con una formación completa y bien estructurada.
En Mateguapo.com te ofrecemos el curso Cálculo Integral en 1 variable (completo), diseñado para que aprendas como un verdadero matemático, pero explicado con un lenguaje claro y moderno.
✅ ¿Por qué estudiar con Mateguapo?
Tú eliges tus tiempos y tu ritmo. Estudia cuando quieras, sin presiones ni horarios.
Explicaciones desde cero, con lógica y claridad. Nada de memorización ciega: aquí entiendes por qué.
Acceso al Grupo de Estudio en Instagram. Resuelve dudas, convive con otros estudiantes y recibe ayuda segura y personalizada.
Contenido creado por matemáticos. No es un curso más de escuela: es matemáticas reales, útiles, y bien explicadas.
📘 Inscríbete ya en Cálculo Integral en 1 variable (completo) en Mateguapo.com📲
Y no olvides seguirnos en instagram.com/@mateguapx para más contenido exclusivo.
¡Nos vemos en clase, guapo matemático!

Comments