¿Por qué los matemáticos preferimos los radianes en trigonometria?

(Spoiler: somos flojos y nos gusta lo elegante)

¿Alguna vez te has preguntado por qué en los libros de matemáticas serios todo está en radianes y casi nunca en grados? ¿Por qué los senos y cosenos se evalúan en cosas como π/4 o π/3, y no en 45° o 60°?

Bueno, la respuesta corta es esta: los radianes hacen que las funciones trigonométricas sean muchísimo más fáciles de manejar… y si algo nos gusta a los matemáticos, es la comodidad elegante (a.k.a. flojera inteligente).

El punto clave: ¿qué demonios es un radian?

Primero hay que aclarar qué es un radian. Un radian es una forma natural de medir ángulos basada en el propio círculo. Si tomas un arco cuya longitud es igual al radio del círculo, el ángulo que forma en el centro mide 1 radian.

Así, un círculo completo tiene 2π radianes. ¿Ves? El número π entra de forma natural al juego. Mientras tanto, el sistema de grados fue una invención algo arbitraria (360 porque sí, porque los babilonios tenían ese rollo con los múltiplos de 60).

¿Y por qué los radianes son más cómodos con las funciones en trigonometria?

Porque las derivadas y las series de Taylor de funciones como seno y coseno solo funcionan bonito si usas radianes.

• Si usamos radianes mira que bonito queda esto:

• Pero si usaras grados, tendrías que multiplicar todo por un factor de conversión molesto

Que feo la verdad.

Todo se ensucia, todo se complica, y nadie quiere eso.

¿Y los matemáticos qué ganamos?

Lo de siempre:

• Cálculo más limpio

• Definiciones más precisas

• Fórmulas que no cambian cada 5 minutos

Por ejemplo, la famosa definición de seno como serie de potencias:

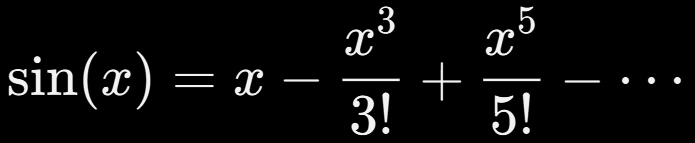
¡Sólo es válida si x está en radianes! Si no, ni siquiera es cierta.

¿Y qué tiene que ver todo esto con las funciones?

Todo. La trigonometría y las funciones están completamente entrelazadas. Cuando analizamos funciones trigonométricas, especialmente en cálculo, el uso de radianes no es opcional… es obligatorio si quieres hacer las cosas bien.

Las gráficas, las derivadas, las integrales… todo tiene más sentido con radianes. Los matemáticos no usamos grados, no porque no podamos, sino porque somos prácticos. Y porque preferimos escribir π/2 que andar dividiendo 90° entre 180 para convertirlo.

Conclusión

Si estás aprendiendo funciones trigonométricas, mejor acostúmbrate ya a los radianes. Vas a ver que todo se vuelve más simple, y tu profe te lo va a agradecer (bueno… tal vez no, pero tú sí te lo vas a agradecer).

¿Quieres aprender más sobre funciones, trigonometría y cómo usar los radianes como un crack?

En Mateguapo.com tenemos el curso de Gráficas y Ecuaciones y próximamente el de Trigonometria (completo), donde te explico todo esto desde cero y con enfoque formal. Pero no aburrido. Formal pero sabroso.

Aqui tienes una clase GRATIS de Cálculo como ejemplo:

Además, en Mateguapo:

• Enseñamos con rigor, con demostraciones y sin atajos raros.

• Te explico todo con ejemplos reales y sin miedo a lo difícil.

• Tienes acceso a la comunidad del Grupo de Estudio en Instagram para resolver tus dudas.

• Y te aseguro que vas a entender de verdad.

Ver Cursos de todos los niveles

¡Allá nos vemos! :)