¿Qué es el Teorema Fundamental del Cálculo?
El Teorema Fundamental del Cálculo es el puente que une dos grandes mundos: el cálculo diferencial y el cálculo integral. Es uno de los resultados más profundos y elegantes de las matemáticas, y su impacto va mucho más allá del aula: permite resolver problemas de movimiento, optimización, física, economía, y más.
En este artículo vas a entender qué dice exactamente el Teorema Fundamental del Cálculo, cómo se interpreta, por qué se considera “fundamental” y cómo se aplica paso a paso. Todo con ejemplos, explicaciones claras y sin complicaciones.

¿Por qué es importante el Teorema Fundamental del Cálculo?
Antes de entrar en el teorema, aclaremos dos ideas clave:
-
El cálculo diferencial estudia cómo cambian las funciones, a través de la derivada.
-
El cálculo integral se encarga de medir áreas, acumulación o sumas infinitas, a través de la integral definida.
El Teorema Fundamental del Cálculo (TFC) une estos dos conceptos: muestra que derivar y luego integrar (o al revés) son procesos inversos, bajo ciertas condiciones.
Enunciado del Teorema Fundamental del Cálculo
Si f es una función continua en un intervalo [a,b], y definimos:
Entonces F es derivable y se cumple:
Esto significa que la derivada de una integral acumulada es la función original. Nos dice que el proceso de “sumar infinitos pedacitos” (integrar) y luego “ver cómo cambia eso” (derivar) te regresa a donde empezaste.

Segunda parte del TFC
Hay una segunda parte de este Teorema que en realidad es un corolario (un resultado derivado del resultado del Teorema).
Si f es continua en [a,b], y F es cualquier función cuya derivada sea f, entonces:
Esto nos da una fórmula práctica para calcular integrales definidas: no necesitas sumar infinitos rectángulos, basta con encontrar una antiderivada y evaluar en los extremos.
Ejemplo simple del Teorema Fundamental del Cálculo
Queremos calcular:
Sabemos que una primitiva de x^2 es:
Entonces:
Gracias al TFC, no necesitamos sumar áreas manualmente: una antiderivada y dos evaluaciones bastan.


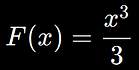
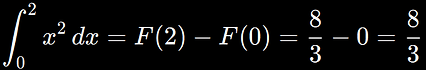
¿Por qué es tan importante el Teorema Fundamental del Cálculo?
Porque transforma por completo nuestra forma de pensar:
-
Nos da una fórmula rápida y exacta para calcular integrales definidas.
-
Justifica que los procesos de derivar e integrar son opuestos.
-
Une dos ramas enteras del cálculo en un solo marco teórico.
-
Es la base de miles de aplicaciones en física, estadística, biología, ingeniería y más.
Sin el TFC, el cálculo integral sería mucho más lento y complejo, y todas las integrales se tendrían que resolver por sumas infinitas.
¿Qué necesitas para entender y aplicar el TFC?
-
Saber derivar funciones comunes.
-
Entender qué es una integral definida.
-
Manejar las antiderivadas (también llamadas primitivas).
-
Conocer funciones continuas y su comportamiento.
Todo esto lo puedes aprender paso a paso en el curso que te recomendamos abajo 👇
Aprende el Teorema Fundamental del Cálculo con Mateguapo
👉 Curso de Cálculo Integral – Mateguapo
En este curso aprenderás:
-
Qué significa realmente integrar y derivar.
-
Cómo usar el TFC para resolver integrales rápidamente.
-
Casos especiales: funciones con discontinuidades, límites, integrales impropias, etc.
-
Ejercicios resueltos con explicación clara y didáctica.
Ideal para estudiantes que ya conocen el cálculo diferencial y quieren llevar sus habilidades al siguiente nivel.
Conclusión
El Teorema Fundamental del Cálculo es más que un resultado técnico: es la llave que abre la puerta a todo el mundo del análisis matemático. Entenderlo te permite conectar ideas, resolver problemas de forma elegante y aplicar el cálculo a situaciones reales.
Y si quieres dominarlo de verdad, paso a paso, con lógica y sin fórmulas memorizadas...
🚀 Empieza hoy el curso de Cálculo Integral en Mateguapo.
