10 Ejercicios Resueltos de Integrales Impropias
- 9 jul 2025
- 2 Min. de lectura
Actualizado: 14 jul 2025
Las integrales impropias son uno de los temas que más confusión causan a los estudiantes. Ya dominaste las integrales definidas e indefinidas, pero llega un punto donde aparecen cosas raras: intervalos infinitos, funciones con asíntotas, valores que "parecen no existir"... y de pronto necesitas un nuevo enfoque.
Este blog es un compendio de 10 ejercicios resueltos de integrales impropias pensados para estudiantes que ya saben integrar, pero quieren poner a prueba su habilidad con estos casos especiales.
🔎 ¿Qué son las Integrales Impropias?
Antes de lanzarnos con los ejercicios, recuerda que una integral impropia ocurre cuando:
El intervalo de integración no es finito (como de 1 a ∞.
La función tiene una discontinuidad vertical (como 1/x en 0).
En estos casos, evaluamos el límite correspondiente y determinamos si la integral converge o diverge.
🧠 Ejercicios Resueltos de Integrales Impropias
1.
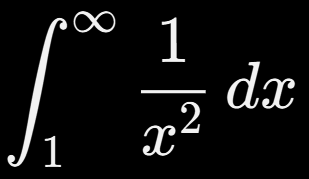
Solución:

✅ Converge
2.

Solución:
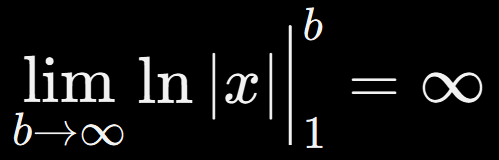
❌ Diverge
3.

Solución:

✅ Converge
4.
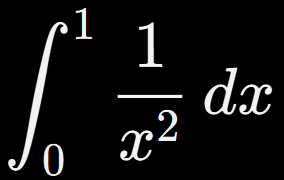
Solución:

❌ Diverge
5.

Solución:
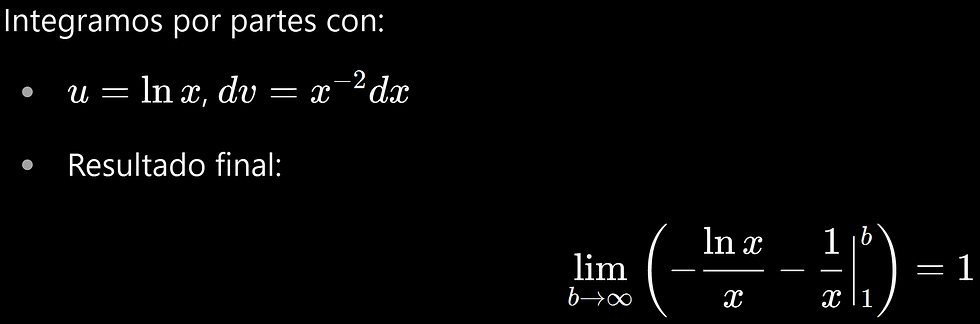
✅ Converge
6.

Solución:

✅ Converge
7.

Solución:

✅ Converge
8.
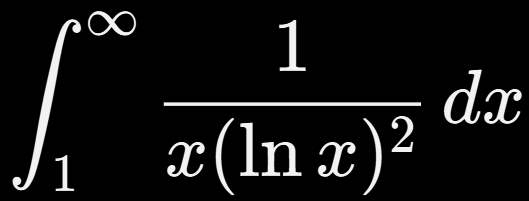
Solución:

✅ Converge
9.
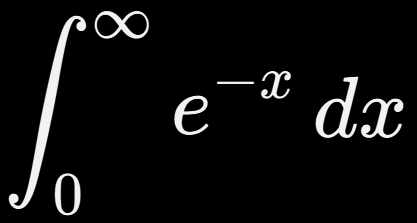
Solución:

✅ Converge
10.

Solución:
Esta es una integral impropia por dos razones:
El intervalo de integración es infinito, pues va de 1 a ∞.
La función sinx/x no tiene primitiva elemental, por lo que no se puede resolver con técnicas de integración directas.
Sin embargo, sí se puede estudiar su convergencia usando el criterio de Dirichlet:
✍️ Criterio de Dirichlet (forma general):
Si f es una función acotada y oscilante (como el seno), y si g es una función monótonamente decreciente (como 1/x) y que tiende a cero, entonces la integral impropia
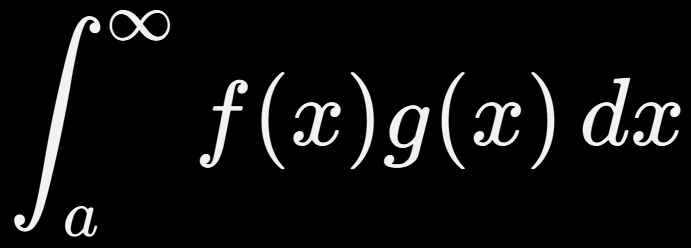
converge.
Aplicamos esto con:

Por tanto, la integral

converge, aunque no se puede expresar con funciones elementales.
✅ Converge
🧮 Conclusión
Las integrales impropias son una herramienta fundamental para entender problemas reales donde hay infinito involucrado o discontinuidades. Saber si una integral converge o no, es una habilidad que puede aplicarse en análisis, física y probabilidad.
Si te gustó esta práctica, recuerda que puedes dominar el cálculo formalmente (con demostraciones y bien hecho) en nuestros cursos.
🚀 Aprende en serio con Mateguapo.com
En Mateguapo.com te explicamos las matemáticas desde un enfoque formal y lógico, con demostraciones, ejemplos visuales y clases dinámicas pensadas para que realmente entiendas lo que estás estudiando.
📚 Álgebra (completo) - desde cero.
Aquí tienes de regalo una clase GRATIS de Cálculo :)
🎯 Ventajas de estudiar con nosotros:
Acceso por el tiempo que necesites, adaptado a ti
Puedes preguntar lo que quieras
Ejercicios explicados paso a paso
Ejemplos reales y útiles
Todo pensado para carreras científicas 🚀
¡Allá nos vemos! 😉



Comentarios