Cómo Diagonalizar Matrices Paso a Paso: Una Guía Clara para Estudiantes de Matematicas

Artemiy Rovinski
6 jul
3 Min. de lectura

¿Alguna vez te has preguntado para qué sirve diagonalizar una matriz? Si estudias matemáticas, te habrás topado con esta técnica poderosa que aparece tanto en álgebra lineal como en muchas aplicaciones avanzadas, desde física hasta economía.

En este blog, te explico cómo diagonalizar matrices, paso a paso, de forma clara y práctica. Si entiendes esto bien, abrirás las puertas a conceptos como cambio de base, formas canónicas, potencias de matrices, y muchas cosas más.

¿Qué es diagonalizar una matriz?

Diagonalizar una matriz significa encontrar una matriz diagonal que sea equivalente (en el sentido de similaridad) a la matriz original. Formalmente, si una matriz cuadrada A se puede escribir como:

A = PDP⁻¹

Entonces decimos que A es diagonalizable, donde:

D es una matriz diagonal (con los valores propios de A en la diagonal),
P es la matriz formada por los vectores propios de A,
y P⁻¹ es la inversa de P.

¿Para qué sirve diagonalizar una matriz?

Diagonalizar matrices tiene muchas aplicaciones prácticas y teóricas en matemáticas:

💡 Calcular potencias de matrices fácilmente: Aⁿ = P Dⁿ P⁻¹

📊 Modelar sistemas dinámicos (como poblaciones, economía o física cuántica).

🧠 Entender cambios de base en espacios vectoriales.

🔬 Analizar estabilidad de sistemas de ecuaciones diferenciales.

¿Cuándo se puede diagonalizar una matriz?

Una matriz se puede diagonalizar si tiene n vectores propios linealmente independientes (donde n es el tamaño de la matriz cuadrada). Es decir, si podemos construir una base de vectores propios del espacio, entonces se puede diagonalizar.

Pasos para diagonalizar una matriz en matematicas

Supongamos que tienes una matriz A de 2×2 o 3×3. Aquí tienes los pasos que debes seguir:

1. Encuentra los valores propios (autovalores)

Resuelve la ecuación:

det( A − λI ) = 0

Este es el polinomio característico de A. Sus raíces son los valores propios λ.

✅ Ejemplo práctico:

Sea la matriz

como digonalizar matrices matematicas algebra lineal

Calculamos det( A − λI ) y resolvemos para λ:

Entonces los valores propios son: λ = 5 y λ = 2 .

2. Encuentra los vectores propios

Para cada valor propio λ, resuelve el sistema:

(A − λI)·v = 0

Esto te dará el espacio propio asociado a λ.

Elige un vector no cero de cada espacio: ese será tu vector propio.

3. Construye la matriz P

Coloca cada vector propio como columna en una matriz P.

4. Construye la matriz D

La matriz D será diagonal, con los valores propios en la diagonal (en el mismo orden que pusiste los vectores en P).

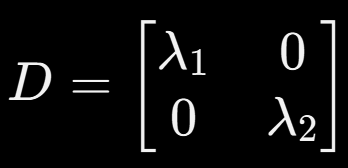
5. Verifica que A = PDP⁻¹

Este paso es opcional pero recomendable para asegurarte de que hiciste todo bien. Calcula P D P⁻¹ y verifica que obtienes nuevamente A.

¿Qué pasa si no se puede diagonalizar?

Si no puedes encontrar suficientes vectores propios linealmente independientes, la matriz no es diagonalizable. Pero no te preocupes: en esos casos, puedes usar otras herramientas como la forma de Jordan (tema para otro blog 😏).

Conclusión

Diagonalizar matrices no solo es una técnica útil, sino una de las más importantes del álgebra lineal. Al dominar este proceso, estarás mucho más preparado para entender transformaciones lineales, sistemas dinámicos, y muchas otras ideas poderosas dentro del mundo de las matematicas.