Convergencia y Divergencia: La Filosofía Detrás de las Integrales Impropias

Las integrales impropias son uno de esos temas en matemáticas que, aunque parecen meramente técnicos, encierran ideas profundamente filosóficas. ¿Cómo puede una cantidad infinita dar un resultado finito? ¿Cuándo una integral tiene sentido, y cuándo no? ¿Qué significa realmente que una integral “converja”?

En este blog, no solo vamos a ver lo que dicen los libros de cálculo, sino que vamos a meternos en el fondo de la cuestión: ¿por qué nos importa tanto que una integral impropia converja o diverja?

¿Qué es una integral impropia?

Para recapitular: una integral impropia es aquella que no cumple con las condiciones estándar de una integral definida. Esto puede suceder por dos razones:

1. Los límites de integración son infinitos (por ejemplo: ∫₁^∞ 1/x² dx)

2. La función tiene una discontinuidad o tiende a infinito en algún punto del intervalo de integración (por ejemplo: ∫₀¹ 1/√x dx)

   
   

Este tipo de integrales no se evalúan directamente, sino como límites. Y ahí empieza lo interesante.

¿Qué significa “convergencia”?

Cuando decimos que una integral impropia converge, nos referimos a que su valor como límite existe y es finito.

Por ejemplo:

Este resultado tiene un sentido real: aunque estamos sumando “una cantidad infinita de cosas”, el total que acumulamos es finito. Y eso es casi poético.

¿Y la divergencia?

Por otro lado, una integral diverge cuando ese límite no existe o es infinito. Por ejemplo:

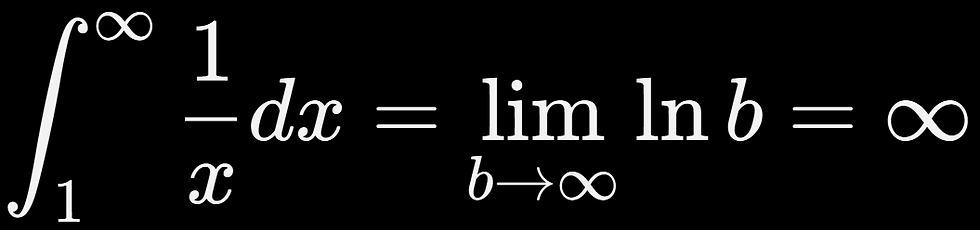
Aquí, la suma crece sin límite, y decimos que la integral no tiene un valor finito. No podemos “contenerla”. La función se desborda.

La filosofía detrás del asunto

🔍 ¿Por qué insistimos tanto en que una integral tenga un valor finito?

Porque la convergencia es una garantía de sentido. Nos dice que podemos modelar, medir o entender un fenómeno incluso si es “infinito” en alguna dirección.

Una integral impropia que converge es como una conversación profunda: se puede extender indefinidamente sin perder el hilo. Una que diverge es más como un grito: fuerte, intenso... pero que no te lleva a ningún lugar claro.

Ejemplos que ilustran esto

1. La distribución de probabilidad normal

La famosa curva de Gauss no está acotada. Pero su integral:

¡Converge! Eso significa que la probabilidad total bajo la curva es 1. Y eso da sentido a todo el modelo.

2. El campo gravitacional de una línea infinita

Imagina una línea de masa que se extiende infinitamente. Puedes calcular su campo usando:

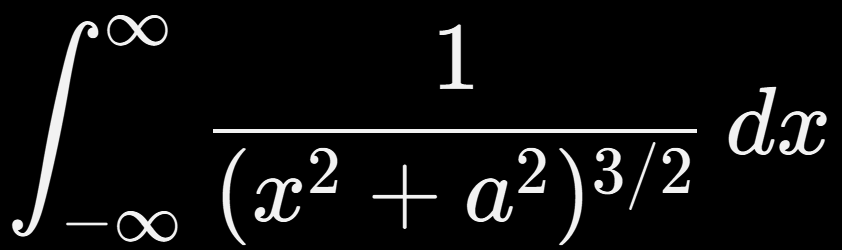
¡Y converge! Eso quiere decir que incluso sistemas infinitos pueden tener efectos totales finitos, medibles y significativos.

¿Y cómo saber si una integral impropia converge o no?

Aquí entran los tests de convergencia, como:

• Comparación directa

• Comparación por límites

• Prueba del p-test (por ejemplo, ∫₁^∞ 1/x^p dx converge si p > 1)

Estas herramientas no solo nos ayudan a evaluar integrales, sino que nos enseñan a discernir cuándo tiene sentido sumar hasta el infinito.

Entonces, ¿cuál es la gran lección?

La convergencia no es solo un tecnicismo: es una validación matemática de que algo aparentemente inabarcable sí puede tener sentido.

Cuando una integral impropia converge, no solo obtenemos un número. Obtenemos una forma de hablar con el infinito y entenderlo con rigor.

¿Te interesa dominar las integrales impropias y todo el cálculo integral?

En Mateguapo.com tenemos el curso perfecto para ti, impartido por un matemático puro:

📚 Cálculo Integral en 1 variable (completo)

Aquí tienes de regalo una clase GRATIS de Cálculo :)

🎯 Ventajas de estudiar con nosotros:

• Acceso por el tiempo que necesites, adaptado a ti

• Puedes preguntar lo que quieras

• Ejercicios explicados paso a paso

• Ejemplos reales y útiles

• Todo pensado para carreras científicas 🚀

Ver Cursos de todos los niveles

¡Allá nos vemos! 😉