Aplicaciones Reales de las Integrales Impropias: De la Física al Análisis de Datos

Artemiy Rovinski
29 jun
3 Min. de lectura

Actualizado: 4 jul

Las integrales impropias son uno de esos temas que, aunque suenen técnicos, aparecen por todos lados en las matemáticas aplicadas. De hecho, si alguna vez te preguntaste cómo calculamos ciertos modelos físicos infinitos, cómo se evalúa el comportamiento asintótico de una función o cómo se estima una probabilidad en estadística... probablemente estabas mirando una integral impropia de frente.

En este blog vamos a explorar algunas de las aplicaciones reales más interesantes de las integrales impropias. Y si te has estado preguntando por qué los matemáticos se toman tan en serio este tipo de integrales, acá tienes las razones.

¿Qué son las integrales impropias?

Una integral impropia es aquella que:

Tiene límites infinitos (por ejemplo, integrar de −∞ a ∞), o
Tiene una función que se hace infinita dentro del intervalo (como integrar 1/x cuando x → 0).

A diferencia de las integrales definidas "normales", en estas hay que tener cuidado: no siempre existen (es decir, convergen) y, cuando lo hacen, lo hacen con estilo.

Aplicaciones en Física

1. Electrostática y Gravitación

La ley de Coulomb y la ley de la gravitación universal describen fuerzas que actúan a distancia infinita. Para calcular el campo eléctrico o el potencial debido a una distribución continua de carga o masa, a menudo se requiere una integral impropia sobre un espacio infinito.

Ejemplo clásico:

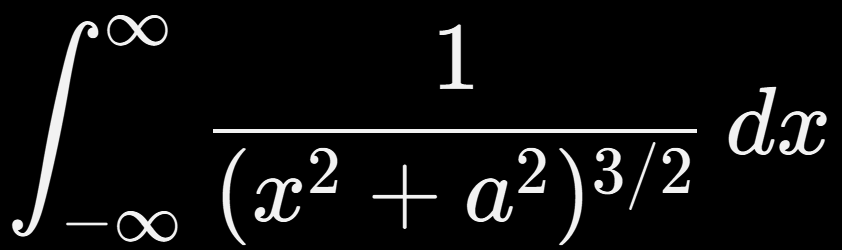
Esta integral aparece al calcular el campo eléctrico de una línea de carga infinita.

2. Mecánica Cuántica

En la ecuación de Schrödinger, se utilizan integrales impropias al calcular funciones de onda normalizadas en todo el espacio:

Este tipo de integral nos dice la probabilidad total de encontrar una partícula en algún lugar del espacio, lo cual es fundamental para la predicción cuántica.

3. Transferencia de calor y ecuación de difusión

Modelos como la ecuación del calor tienen soluciones que incluyen la función de Gauss, cuya integral sobre todo el espacio debe converger:

Este resultado no solo es elegante, sino que se usa literalmente en la predicción de cómo se propaga el calor o una sustancia en un medio.

Aplicaciones en Análisis de Datos y Estadística

4. Distribución normal

La famosa campana de Gauss es una función cuya integral total (sobre todo el eje real) es 1, es decir:

Esto es esencial para calcular probabilidades continuas en estadística.

La curva no está acotada, pero su integral sí: ¡esa es la magia de las integrales impropias!

5. Técnicas de regularización en Machine Learning

Cuando trabajamos con modelos de regresión que involucran parámetros continuos, o cuando usamos kernels para métodos como SVM o Gaussian Processes, muchas veces se emplean integrales impropias para definir distribuciones o penalizaciones en espacios infinitos.

Ejemplo: una función de penalización que decae con la distancia puede involucrar:

Este tipo de expresión ayuda a “domar” el comportamiento del modelo y hacerlo más estable.

¿Por qué son tan importantes?

Las integrales impropias nos permiten:

✅ Calcular modelos que se extienden al infinito

✅ Analizar singularidades sin perder la cabeza

✅ Aterrizar probabilidades y comportamientos en espacios reales

✅ Conectar la teoría matemática con las ciencias aplicadas

Conclusión

Lejos de ser solo una curiosidad técnica, las integrales impropias son herramientas poderosísimas que atraviesan disciplinas enteras: de la física teórica a la estadística, pasando por el aprendizaje automático y más allá.

Por eso en Mateguapo.com, en nuestro curso de Cálculo Integral en 1 variable (completo), abordamos este tema con rigor, claridad y muchas aplicaciones. Porque sí, saber integrales impropias cambia tu forma de ver el mundo.