Las 5 integrales impropias más famosas (y por qué son tan interesantes)

Artemiy Rovinski
13 jun
2 Min. de lectura

Actualizado: 4 jul

Cuando hablamos de integrales impropias, entramos a un mundo de matemáticas donde las cosas se ponen emocionantes: aparecen infinitos, puntos donde la función explota (o desaparece) y donde la intuición a veces falla. En este blog quiero enseñarte 5 de las integrales impropias más famosas, que seguro has visto en algún libro o clase... ¡o que pronto verás si sigues aprendiendo!

1️⃣ La integral de 1/x

Es probablemente la más clásica de todas las integrales impropias. Al evaluar, tenemos:

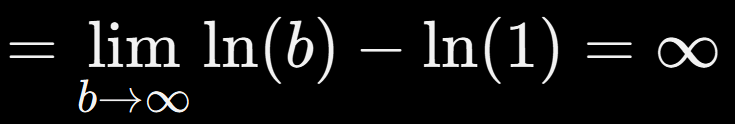
Esto nos muestra que esta integral diverge. Aunque la función decae, lo hace demasiado lento como para tener un área finita bajo la curva. ¡Un clásico para entender cuándo las integrales impropias no convergen!

2️⃣ La integral de e^(-x)

Esta es de las primeras integrales impropias que se estudian porque sí converge:

Su área bajo la curva es finita, y es básica en probabilidad (la famosa exponencial).

3️⃣ La integral de 1/x^2

Aquí la función decae más rápido que 1/x, y por eso sí tenemos:

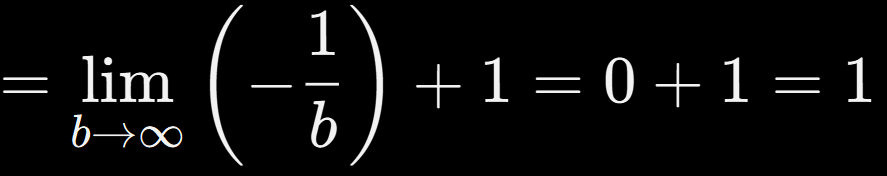
¡Perfecto ejemplo para ver cómo el exponente en el denominador marca la diferencia!

4️⃣ La integral de 1/sqrt(x)

En este caso la integral es impropia porque el integrando se va al infinito cuando x→0. Pero aún así:

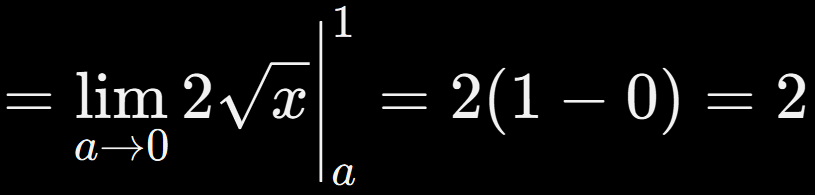
Una de las favoritas en cursos de cálculo para estudiar integrales con singularidades en un extremo.

5️⃣ La integral gaussiana

Esta integral no solo es famosa, ¡es legendaria! Su valor es:

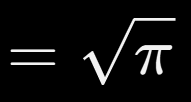
Pero lo más interesante es que no se resuelve con técnicas básicas de cálculo, sino que requiere un truco en dos dimensiones. Aparece en estadística y física por todos lados.

💡 ¿Por qué nos gustan las integrales impropias?

Porque nos ayudan a entender cómo se comportan las funciones en los extremos, cómo manejamos el infinito o los puntos problemáticos. Además, son la base de muchas aplicaciones reales: economía, física, probabilidad, ingeniería... ¡y hasta inteligencia artificial!