¿Por qué el logaritmo natural es el más importante de los logaritmos en matemáticas?
- Artemiy Rovinski

- 19 may
- 2 Min. de lectura
Actualizado: 4 jul
Si alguna vez has visto ln(x) y te has preguntado qué tiene de especial, prepárate: el logaritmo natural es uno de los conceptos más potentes y elegantes de las matemáticas. Detrás de esa simple abreviación se esconde una conexión profunda entre la función exponencial, el cálculo y muchos fenómenos del mundo real.

¿Qué significa exactamente ln(x) ?
El logaritmo natural es simplemente el logaritmo de base e, es decir:

donde e ≈ 2.71828 (aproximadamente) es un número irracional que aparece en una enorme cantidad de contextos matemáticos.
¿Y por qué? Porque describe el crecimiento continuo perfecto.
En palabras simples: si el logaritmo responde a la pregunta “¿qué exponente necesito para llegar a cierto número?”, entonces ln(x) responde a esa pregunta pero usando la base más natural para el crecimiento: el número eee.
¿Por qué e y no otra base?
En la función exponencial f(x)=a^x, si eliges a=e, ocurre algo mágico: su derivada es ella misma:

Esto la convierte en la única función exponencial que no cambia su tasa de crecimiento. ¡Una propiedad increíblemente útil en cálculo!
Y como los logaritmos son la inversa de las funciones exponenciales, entonces el logaritmo natural es el compañero perfecto para trabajar en problemas de derivadas, integrales, límites y más.
Aplicaciones del logaritmo natural
El ln(x) no está ahí por estética: aparece en todo tipo de problemas de la vida real y de las matemáticas avanzadas. Por ejemplo:
Crecimiento poblacional continuo
Modelos financieros (como el interés compuesto)
Física (decaimiento radioactivo, leyes de enfriamiento)
Cálculo (resolución de integrales complejas)
Probabilidades (entropía, distribuciones continuas)
Cuando te sumerges en el mundo de las funciones exponenciales y los logaritmos, el ln(x) se vuelve una herramienta natural y poderosa.
¿Y qué hay de las integrales?
Uno de los resultados más bonitos del cálculo integral es:
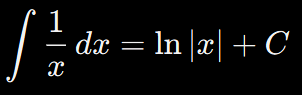
¡Sí! El logaritmo natural aparece como el resultado directo de integrar una función racional simple. Y esto no es coincidencia: esta función es esencial para entender áreas bajo curvas y transformaciones logarítmicas.
En resumen
El logaritmo natural no es solo una base más. Es una de las ideas más elegantes de las matemáticas, con conexiones profundas a la función exponencial, al cálculo y al mundo real. Comprenderlo es un paso clave para dominar el lenguaje matemático moderno.
Domina estos temas en Mateguapo
Si quieres ir más allá y entender de verdad cómo se usan los logaritmos, las funciones exponenciales y su papel en el cálculo, te invito a los cursos de:
No son unos cursos más: es tu guía clara para entender las matemáticas desde lo fundamental hasta lo poderoso.




Comments