¿Qué es una Integral Generalizada y cómo se relaciona con las Integrales Impropias?

Artemiy Rovinski
9 jul
3 Min. de lectura

Cuando empezamos a estudiar cálculo, aprendemos a integrar funciones en intervalos cerrados y acotados, con funciones bonitas y bien portadas. Pero ¿qué pasa cuando algo no está bien definido? ¿Cuándo la función explota o el intervalo es infinito? Entra en juego un concepto fundamental: las integrales generalizadas, también conocidas como integrales impropias.

En este blog te explico qué son, cuándo aparecen y cómo se resuelven paso a paso. Si alguna vez te preguntaste qué significa realmente integrar hasta el infinito (o hasta un punto donde la función se hace infinita), aquí tienes la respuesta.

¿Qué es una Integral Generalizada?

Una integral generalizada es un tipo de integral que no cumple con todas las condiciones del Teorema Fundamental del Cálculo. Esto puede deberse a dos razones principales:

El intervalo de integración no está acotado (por ejemplo, de 1 a ∞.
La función integrada no está acotada en algún punto del intervalo (por ejemplo, tiene una discontinuidad infinita)

En ambos casos, la integral no está definida directamente, pero podemos intentar definir su valor como el límite de una integral definida. Es decir, usamos límite + integral común para darle sentido.

¿Y entonces qué son las Integrales Impropias?

💡 ¡Sorpresa! En realidad, "integral impropia" es otro nombre para una integral generalizada. Ambas se refieren al mismo fenómeno: integrales en las que hay algo fuera de lo común. Lo que pasa es que "impropia" suena un poco más rebelde.

Tipos de Integrales Impropias (o Generalizadas)

Veamos los dos tipos más frecuentes:

1. Cuando el intervalo es infinito

Ejemplo:

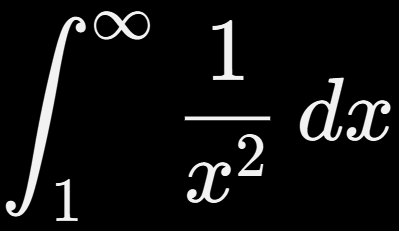
Esta integral no termina nunca, pero su área bajo la curva se puede calcular si el límite existe:

✅ ¡Converge!

2. Cuando la función explota

Ejemplo:

Aquí la función tiene una discontinuidad infinita en x=0x = 0x=0. Lo resolvemos así:

✅ También converge.

¿Para qué sirven las Integrales Impropias?

Te sorprendería saber cuántos modelos del mundo real usan este tipo de integrales:

Para calcular probabilidades en distribuciones infinitas (como la normal).
En física, cuando se mide energía o masa en espacios infinitos.
En economía, para calcular valores presentes con tasas de descuento a largo plazo.
En teoría de señales y transformadas como Fourier y Laplace.
Y hasta en el estudio de series infinitas o soluciones de ecuaciones diferenciales.

Si las integrales definidas son el pan, las impropias son el mole: no son para todos los días, pero cuando aparecen, ¡se roban el show!

¿Cómo saber si convergen o divergen?

El truco está en usar límites, comparaciones o criterios como el de p-series o Dirichlet. Aquí no hay recetas mágicas, pero sí una técnica muy poderosa: comparar tu integral con otra cuya convergencia ya conozcas.

Conclusión

Las integrales impropias o generalizadas son una herramienta poderosa para extender el concepto de área incluso cuando la intuición clásica deja de funcionar. Saber cuándo una integral tiene sentido (y cuándo no) es una habilidad clave en matemáticas avanzadas, y dominar este tema te abrirá muchas puertas, especialmente si te interesa la física, la estadística o el análisis.